Twist-angle two-dimensional systems, such as twisted bilayer graphene, twisted bilayer transition metal dichalcogenides, twisted bilayer phosphorene and their multilayer van der Waals heterostructures, exhibit novel and tunable properties due to the formation of Moiré superlattice and modulated Moiré bands. The review presents a brief venation on the development of “twistronics” and subsequent applications based on band engineering by twisting. Theoretical predictions followed by experimental realization of magic-angle bilayer graphene ignited the flame of investigation on the new freedom degree, twistangle, to adjust (opto)electrical behaviors. Then, the merging of Dirac cones and the presence of flat bands gave rise to enhanced light-matter interaction and gate-dependent electrical phases, respectively, leading to applications in photodetectors and superconductor electronic devices. At the same time, the increasing amount of theoretical simulation on extended twisted 2D materials like TMDs and BPs called for further experimental verification. Finally, recently discovered properties in twisted bilayer h-BN evidenced h-BN could be an ideal candidate for dielectric and ferroelectric devices. Hence, both the predictions and confirmed properties imply twist-angle two-dimensional superlattice is a group of promising candidates for next-generation (opto)electronics.
From the successful fabrication of atomically thin carbon films by Andre Geim and Konstantin Novoselov through mechanical exfoliation in 2004, graphene not only verified the possibility for stable existence of two-dimensional materials but also exhibited novel and outstanding physical properties including ultra-high carrier mobility, ultra-high thermal conductivity and superior mechanical properties, which was awarded the Nobel prize in physics 2010. Subsequently, investigations on exploring new 2D materials and their applications have become the frontier fields in condensed physics, such as graphyne, two-dimensional transition metal dichalcogenides (TMDs) , MXenes , hexagonal boron nitride (hBN) , black phosphorene (BP) , black arsenic . By breaking the weak van der Waals interaction between layers as a “top-down” method like exfoliation or aggregating atoms together as a “bottom-up” method like chemical vapor deposition, researchers have developed variable methods to produce versatile two-dimensional materials and fabricated diverse devices like a field-effect transistor, photodetector and PN diode based on their suitable electronic structures and atomic size along the out-of-plane direction.
Undoubtably, as the first discovered and the most popular 2D material, graphene has attracted the most attention on its physical properties and the exploration for more potential applications. For instance, recently, graphene was even used as a holder for transmission electron microscopy or just vertically stacked to serve as a kind of thermal interface material. Now it is generally accepted that after getting rid of interlayer interaction, electrons in graphene around the Fermi level will follow linear energy dispersion, which is supposed to be described by Dirac equation, indicating zero static mass theoretically. However, the semi-metal behavior induced by the lack of bandgap significantly confined the application of graphene in electronics. Therefore, versatile accesses, which contain doping, oxidization, stacking with other 2D materials to form van der Waals heterojunctionsor twisting bilayer graphene, were focused on band engineering in order to obtain new electrical properties. Among them, twisting has irreplaceable merits, providing an impurity-free single-material platform and the presence of a new freedom degree to the system, twistangle (Fig. 1(a) and 1(b)).
In next three years, from the twist-angle disorder in TBG to tunable strongly coupled superconductivity in magic-angle twisted trilayer graphene (MATTG), further to tunable correlated states in twisted bilayer–bilayer graphene (TBBG) , “twistronics” has been extended to multilayer systems. Moreover, after observation of novel physical properties including Pomeranchuk effect, nematicity, Hund’s coupling and Chern gaps and even odd integer quantum Hall states with interlayer coherence in magic-angle or twist-angle graphene systems, the application of MATBG on quantum devices including Josephson junction and single-electron transistor were finally developed recently. This implies that the research interests on twisted graphene may turn to thicker samples with different twist-angles in order to dig deeper in this field.
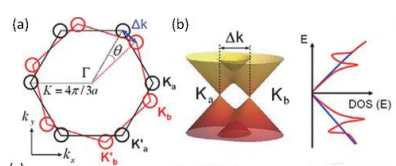
Fig1
Analogously, in twisted bilayer transition metal dichalcogenides (TBTMDs) structures, owing to the comparability between Coulomb interactions and narrow bandwidth, flat bands and correlated states have also been discovered in recent years, which could lead to Mott-like insulator states, topological insulator phases and even superconductor states , proving that TBTMDs nearly recur the novel physical properties of MATBG and certifying the feasibility to popularize the twist-angle-induced band engineering to more 2D materials.
Because of the convenient operation and superior controllability of twisting, which can maintain intrinsic features and bring novel properties simultaneously, twist-induced Moiré pattern in the superlattice became an outstanding platform for study on twist-angle-dependent properties. It is well known that when two 2D lattices with similar periodicity and pattern are stacked followed by twisting relatively, the Moiré superlattice will be formed in which new periodic units with several orders of magnitude larger area will replace the intrinsic unit to bring new periodicity but similar shape of repetitive cell to the bilayer system (Fig. 3(a)), followed by the presence of Moiré potentials as substitution for pristine crystal potential, shown in Figs. 3(b)–3(d).
On one hand, owing to the different spatial configuration in different stacking modes, carriers moving in the Moiré superlattice will feel like a different chemical environment, resulting in the imparity of electronic structure and the presence of periodic Moiré potentials in real space which will exert great influence on carrier transportation (Figs. 4(a) and 4(b)). On the other hand, from the perspective of momentum space, the Moiré superlattice with a much larger scale is corresponded to smaller Brillouin zone due to the reciprocal relation between real space and momentum space, hence tailoring the pristine band structure and modifying the interlayer coupling through creating hybridization among the bands from individual layers.