The family of ABO3 perovskites forms an important class of materials with scientifific value in several technological applications. Understanding the thermal properties of these materials helps determine difffferent high-temperature applications such as thermal barrier coatings and thermoelectric devices. In this work, the thermal properties of the perovskites BaHfO3, BaSnO3, BaZrO3 and KTaO3 are studied using fifirst-principles calculations. Each crystal was confifirmed to be stable by phonon dispersion, and then the lattice contribution to thermal conductivity was calculated for each. BaZrO3 was found to have the lowest thermal conductivity of 5.291 W m−1K−1 at 300 K and decreases to 1.092 W m−1K−1 at 1500 K. BaHfO3 was found to have a thermal conductivity of 8.422 W m−1K−1 at 300 K and decreases to 1.728 W m−1K−1 at 1500 K. BaSnO3 was found to have a thermal conductivity of 6.433 W m−1K−1 at 300 K and decreases to 1.334 W m−1K−1 at 1500 K. KTaO3 was found to have a thermal conductivity of 17.793 W m−1K−1 at 300 K and decreases to 3.649 W m−1K−1 at 1500 K. These results are quite comparable to experimental results at low temperature, however, are seriously underestimated at high temperatures.
As the advancement of technology increases, the discovery of specialized materials with specifific properties will be crucial to the development, performance and effiffifficiency of new devices. The investigation of new materials is fueled by combined theoretical and experimental efffforts, that are driven by both commercial and scientifific motivations. The thermal properties of a material is just one of the properties considered in determining the possible applications of a material from an engineering perspective. More specififically, the thermal conductivity, κ, is the property that describes how heat is transferred by conduction within a material. In nonmagnetic materials, the heat carriers are phonons and electrons, where the phonons dominate for semiconductors and insulators. The portion of the total thermal conductivity that comes from the phonons is defifined as the lattice thermal conductivity, and is denoted κl . Materials with customized κl are used in technologies such as thermal barrier coatings and thermoelectrics.
The ABO3-type perovskites have high cubic symmetry and only fifive atoms in the unit cell. The ’A’ atoms sit at the corners of a cube, the ’B’ atoms sit in the center of the cube, and the oxygen atoms sit at the center of the faces of the cube (see Figure 1.1 for an illustration).
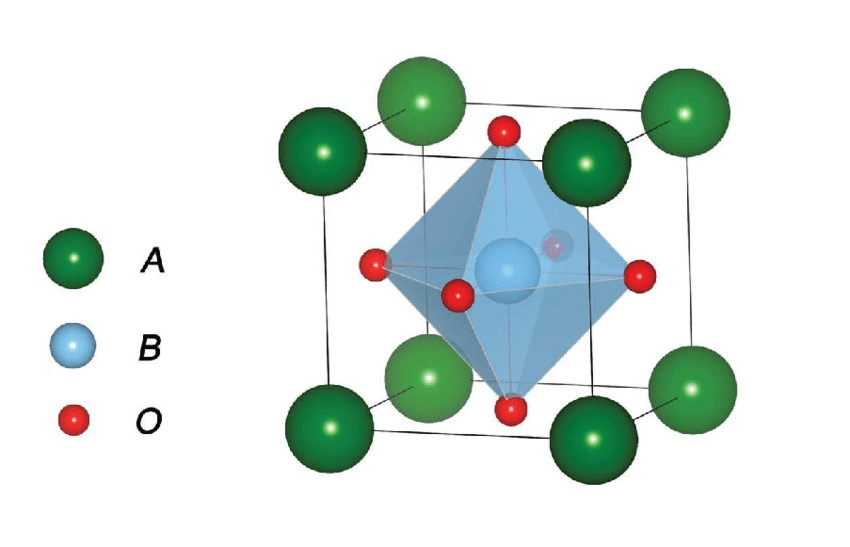
Fig1
This family of materials has drawn much interest because this structure can accommodate many difffferent choices for the atoms in solid solution. The variability in composition leaves a wide range of possibilities when it comes to the macroscopic properties for engineering applications and material design. Studies have shown that many difffferent compositions of ABO3 perovskites have high stability and low thermal conductivity at high temperatures. More specififically, in terms of the computational methods utilized in this research, we aim to take advantage of the high symmetry and simple unit cell (i.e., fifive atoms) as this will reduce the number of computational steps needed for our calculations. In this thesis, we will discuss the results of fifirst-principles calculations of the lattice contribution to thermal conductivity for four ABO3 perovskites. The structures of interest include BaZrO3, BaHfO3, BaSnO3, and KTaO3. Each material was found to have a bandgap so that the lattice thermal conductivity will be dominant in contributing to the total thermal conductivity. Also, each material was confifirmed to be stable by phonon dispersion before third order interatomic force constants (IFC’s) and thermal calculations.
For second-order IFC’s, PHONOPY reads the optimized structure and uses crystal symmetry operations to generate a reduced set of structures that contain atomic displacements (0.01 ˚A). VASP is used to calculate the forces involved with each atomic displacement. After force calculation, PHONOPY then expands the set of atomic displacements from the primitive cell to the supercell using crystal symmetry, and then the elements of force constants between atoms in a primitive cell and the supercell are fifit to the symmetry expanded forces of atoms in supercells.
Similar to PHONOPY, thirdorder.py reads the optimized structure and can generate displacement structures for VASP to calculate force. However, for thirdorder force constants, force contributions from more than just the nearest neighbors are considered. The cut-offff parameter for the contribution is either specifified in real space distance or by n-th nearest neighbor (n ≥ 2) and must be converged for the desired property. VASP is used in the same way as for the second-order IFC’s to calculate the forces corresponding to each displacement, and then thirdorder.py will collect the forces and calculate the third-order IFC’s .