The electronic, optical and thermodynamic properties of ABO3 (A ¼ La,Sr, B ¼ Fe,Co) perovskites are investigated using fifirst-principles calculations. The obtained results indicate that SrCoO3 and SrFeO3 are metals, while LaCoO3 and LaFeO3 are insulators and all of them exhibit strong hybridization of the Fe/ Co-3d and O-2p orbitals. By correlating the energy band structures with the peaks of the imaginary part of the dielectric function, we obtained the origin of each electron excitation to provide information about the active bands for the corresponding optical transitions observed in the experiment. Moreover, the Debye temperatures qD obtained from the phonon frequencies are comparable to the available data. Finally, the thermodynamic properties of the Helmholtz free energy F, entropy S, and constant-volume heat capacity Cv are investigated based on the phonon spectra.
Perovskites in the form of ABO3 (A ¼ alkaline-earth metal or La, B ¼ 3d transition metal) are a plentiful family of compounds, which exhibit novel properties, such as colossal magnetoresistance, ferroelectricity and superconductivity, which make them attractive in technological applications such as in catalysis, sensor devices, magnetoresistance devices and spintronics.1–6 The extensive investigations into ABO3 not only have technical importance, but also originate from the fundamental interest in the physics of their multiple phases. In the ABO3 system, the A sites are divalent or trivalent metals, occupied for example by Sr or La atoms. Correspondingly the B sites are tetravalent or trivalent atoms, occupied for example by Co or Fe atoms, resulting in perovskites with desired properties and performances. Usually, the B cations generally determine the physical properties by either the localized or collective behavior of the d electrons. Of course, the valency of the B sites depends on the valency of the A cations, by which the valency of the B transition metal ions change and thus lead to unusual electronic and magnetic properties.
It is known that all of the optical constants, such as the refractive index n and the extinction coeffiffifficient k, can be derived from the dielectric function 3 ¼ 31(u)+i32(u). The imaginary part 32(u) of the dielectric function is calculated from the momentum matrix elements between the occupied and unoccupied wave functions. The real part 31(u) of the dielectric function is evaluated from the imaginary part 32(u) by the Kramers–Kronig relationship.
ABO3 compounds contain a rich family of crystal structures, such as simple cubic, tetragonal, orthorhombic, rhombohedral etc. Moreover, the structure of one given ABO3 compound is complicated due to phase transitions at difffferent temperatures. For example, the structure of LaFeO3 changes from an orthorhombic Pbnm phase to rhombohedral R3c at 1228 K and subsequently to cubic Pm3m at 2140 K.25 Considering that the properties of the ground state at 0 K are investigated by DFT, we used the crystal structures reported from experiments at low temperatures. SrCoO3 has a perfect perovskite cubic structure with the space group Pm3m 7 (Fig. 1(a)). SrFeO3 has a little distortion to a tetragonal structure with space group P4/mmm 12 (Fig. 1(b)). For compounds with smaller A site ionic radii, the crystal structures of LaCoO3 and LaFeO3 are more distorted to a rhombohedral R3c structure14 (Fig. 1(c)) and an orthorhombic Pbnm structure25 (Fig. 1(d)), respectively. Similarly, the magnetic structures used here are the ground states at low temperatures both from experiment and theory, that are the ferromagnetic structure for SrCoO3, 8–11 the nonmagnetic structure for LaCoO3 (ref. 15, 20 and 29) and the G-type antiferromagnetic structure for LaFeO3. 26–28 For SrFeO3, the ground magnetic state is a noncollinear antiferromagnet with a spiral structure, as shown by experiment.13 Since the non-collinear magnetic ordering has little inuence on the optical and thermodynamic properties, and ferromagnetism has been claried to be the most stable state among all collinear magnetic phases,9,41 we selected ferromagnetism as the magnetic structure of SrFeO3 in the following calculations.
Based on the lattice parameters from the experiment, a full structural optimization was performed using GGA, GGA+U and LSDA+U methods. As shown in Table 1, the lattice constants obtained by GGA+U are much closer to the experimental values than for those obtained by GGA, even for SrCoO3 and SrFeO3 with metal characteristics. Therefore, the correlation U is necessary for the correct prediction of structural information and the following properties which are sensitive to the nestructure. In addition, within the LSDA+U method, lattice constants are signicantly underestimated compared to those obtained by the GGA+U method and experimentally. Therefore, we selected the most suitable method, GGA+U, for further calculations.
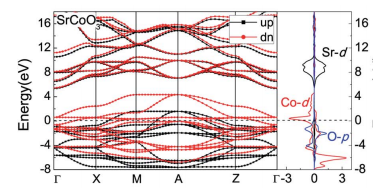
Fig1
Furthermore, the thermodynamic functions can be obtained by the phonon spectrum, assuming that the lattice vibrational degrees of freedom play a more noticeable role than the electronic degrees of freedom. As shown in Fig. 6, the temperature dependence of the Helmholtz free energy F, entropy S, and constant-volume heat capacity Cv are calculated within the harmonic approximation. With an increase in temperature, the free energy decreases, while both the entropy and heat capacity increase from zero at 0 K, all of which conform to the third law of thermodynamics. Moreover, at low temperatures that are much lower than the Debye temperatures, the constant-volume heat capacity Cv is proportional to temperature T3 . The contribution of the lattice heat capacity at low temperatures is mainly from the long wavelength vibration modes of the lattice, which could be approximated by treating the lattice as a continuum. However, at high temperatures, Cv tends to the Dulong–Petit classical limit which is proportional to the number of atoms per unit cell.
This work was supported by the National Science Foundation of China under Grant No. 11534012, and U1230202 (NSAF), the special Funds for Major State Basic Research Project of China (973) under Grant No. 2012CB933702 and the Director Grants of CASHIPS. The calculations were partly performed in the Center for Computational Science of CASHIPS, the ScGrid of the Supercomputing Center and the Computer Network Information Center of the Chinese Academy of Sciences, and partly using the Tianhe-2JK computing time award at the Beijing Computational Science Research Center (CSRC).