The lack of transparent optical components at short wavelengths limits the available wavelengths in Deep Ultraviolet lithography, while the required minimum feature on wafer continues to shrink towards deeper sub-wavelength scales. This places a serious limitation on Kirchhoff boundary conditions that replace the field on the mask openings by the incident field, since this approximation fails to account for the increasingly important topographical effects (thick mask effects) in the computation of the lithographic image. In this paper we present a sophisticated version of Kirchhoff approximation capable of modelling rigorous near field effects while retaining the simplicity of the scalar model. Our model is based on a comparison of the fifields produced by both the thick and ideal thin masks on the wafer. Polarization and edge diffraction effects as well as phase and transmission errors, are included in our model.
In the past few years, the lithographic process entered for the first time into the subwavelength regime of operation. This means that the minimum feature of the printed circuit on wafer is smaller than the wavelength of the light source, limited to 157nm by the lack of refractive lenses in Deep Ultraviolet Lithography (DUVL). Several sophisticated extensions of binary masks have been progressively added over the last decade, such as Phase Shifting Masks (PSM), to enhance resolution while reducing the printable Critical Dimension (CD). Simulation of aerial image formation however, relied entirely on Kirchhoff Boundary Conditions to approximate the fifield immediately behind the patterned mask with an equivalent scalar binary model (Thin-mask approximation). The advantageous simplicity of the Kirchhoff model allows fast, yet reasonably accurate calculations for feature sizes much larger than the source wavelength, but turns out very inaccurate at subwavelength dimensions where topography effects arising from the vector nature of light become noticeable.
Some of these thick-mask effects: polarization dependence due to the different boundary conditions for the electric and magnetic fields, transmission error in small openings, diffraction edge effects or electromagnetic coupling, become particularly critical for Alternating Phase-Shifting masks (Alt. PSM) since they are based on the modulation of both amplitude and phase of the em field propagating through them. Consequently, resourceconsuming rigorous 3D electromagnetic field simulations have become necessary in aerial image formation of an Alt PSM mask, raising the demand for accurate but still simple physical models.
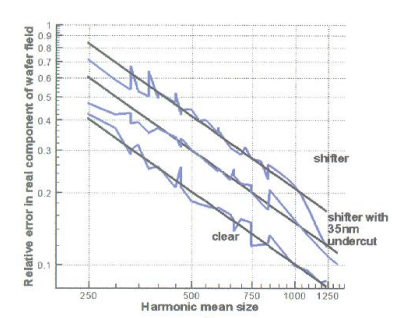
Fig1
Finally, the superposition of both real and imaginary parts of the model give the final Boundary Layer as sketched in figure 5(c), with the parameters of width and transmission coefficient outlined in Table 1. The boundary layer parameters were obtained, for each etching profile, from the slope of the best fitting straight line to the data points, in a least squares sense.
Since the lithographic industry utilizes photomask pattern designs with features comparable to the illumination wavelength, in an attempt to push the limits of optical resolution, rigorous simulation of mask topographic effects become necessary. In practice, however, the numerical effort required to evaluate Maxwell equations on even relatively small mask areas is too high and reliable modelling of these thick mask effects has turned out to be challenging.