硅的湿法化学刻蚀机理

ABSTRACT  

We review what can be said on wet chemical etching of  single crystals from the viewpoint of the science of  crystal growth. Starting point is that there are smooth  and rough crystal surfaces. The kinetics of smooth faces  is controlled by a nucleation barrier that is absent on  rough faces. The latter therefore etch faster by orders of  magnitude. The analysis of the diamond crystal structure  reveals that the { 11 1) face is the only smooth face in this  lattice - other faces might be smooth only because of  surface reconstruction. In this way we explain the  minimum of the etchrate in KOH:H20 in the <001>  direction. Two critical predictions concerning the shape  of the minimum of the etchrate close to <001> and the  transition from isotropic to anisotropic etching in  HFHN03 based solutions are tested experimentally. The  results are in agreement with the theory.

I. INTRODUCTION  

Anisotropic wet chemical etching of single crystalline  silicon, gallium arsenide and quartz is one of the key  technologies for the fabrication of microsystems. Yet the  strong anisotropy of the etchrate in particular etching  solutions (e.g. KOH:H20, EDP, TMAH), and the  isotropy in others (e.g. HFHN03:HzO) is poorly  understood. Mostly the anisotropy of the etchrate is  related to chemical reactions on the crystal surface  oriented in different crystallographic directions. In this  respect maybe the most advanced picture has been  proposed by Seidel et al. 111. They assumed that the  complex formed by the attachment of an OH-ion to the  dangling bond, after the electron has been delivered to  the solid state, changes the back-bond energy of the  silicon atom with three back-bonds in a different way  than iin the situation when one has two OH attached to  the silicon atom with two back-bonds. The difficult point  however is that the silicon atoms have three backbonds  also in the flat  face, not only in the flat  face;  therefore, etchrate and activation energy in these  crystallographic directions should be comparable in  contrast to experimental evidence.

In this paper we add a number of new experimental  results which support the view given here. In particular,  we have looked with greater detail at the dependency of  the etchrate of silicon etched in KOH on the  crystallographic orientation close to the <loo> direction,  and we studied the transition to anisotropic silicon  etching in HFHN03:CH3COOH.

11. THEORY 

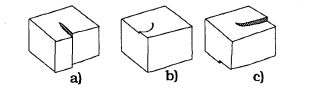
 In kinetics of crystal growth active sites for growth and  dissolution play a key role. These active sites are atoms  with as many bonds to the crystal as to the liquid (or  gaseous) environment. Such a site is called a kink site.  An atom in a kink site in a simple cubic lattice is shown in  fig. la. The heavy shaded atom has three bonds to the  crystal and three bonds to the liquid. In a dissolution  situation it is commonly believed that this atom will  diffuse over the surface (fig. lb), until it either finds a  kink position again or it desorps and diffuses away from  the crystal in the liquid phase (indicated in fig. IC). In a  growth situation, an atom diffuses from the liquid to the  crystal (fig. IC), it diffuses over the crystal surface (fig.  1.b) until it is either desorped or it finds a kink site (fig.  la).

Fig. 1 Illustration of kink sites and the elementary kinetic  processes for etching  @om a to c) and for growing from c to a) crystak

Kinetic rates (for growth and dissolution) thus depend  critically on the number of kink sites on a crystal surface.  This aspect was neglected so far in the discussion of etch  rates of single crystals such as silicon, quartz and GaAs.  Only parts of the total process have been considered: the  chemical reaction rate (which is important for the  adsorption process and the kink integration process,  erroneously considered anisotropic), diffusion in the  liquid solution (isotropic), and the thickness of the  boundary layer. In our view, the most prominent  anisotropy effect is due to the number of kink sites.

Consider the energy difference of the two situations  depicted in fig. 2. In fig. 2.a we show the (111) silicon  surface as one obtains by simply cutting the crystal along  the (111) plane. The dangling bonds are indicated by  light dots. In fig. 2.b we have cut one atom out of the  surface and placed it back somewhere else on the crystal  surface. To do this one has to cut three bonds of strength + each, but one bond is delivered by placing back the  atom onto the surface. The energy difference △E = 2Φ.

Fig. 2 Energy required to create a cavity-adatompair on an  unreconstructed {lll) face of the diamond lattice. △E = 2Φ

This is very much diffeent from the {00l) silicon face as  can be seen in fig. 3. The same operation - creating an  adatom-cavity pair - now costs no energy, because one  has to break two bonds in order to remove an atom from  the (001) face, but one gets them back by placing it back  to any position on this face.

Fig. 3 EnergV required to create a cavity-adatom pair on an  unreconslructed {OOll face in the diamond lattice. △E = 0 

The energy difference AE divided by kT (absolute  temperature times Boltzmann constant) is known as the  a-factor of Jackson (see, e.g. 131) and plays a key role in  theory of crystal growth. At sufficiently low temperature  kTa is proportional to the step free energy y. The  essential difference between the (111) and the (001)  silicon face is: In equilibrium the { 111) face is smooth at  sufficiently small temperature and the (001) is rough.  The step free energy y is finite of the { 11 1 } , and zero of  the (001) face of silicon. The number of cavity - adatom  pairs is proportional to exp -a. This number is very small  on the (111) silicon face at low temperature, but 1 on  the (001) silicon face at any temperature.

111. EXPERIMENTS

111.1. Anisotropic etching  From (iv) of section I1 it follows that the etchrate E and  growth rate G vary proportional to the absolute value of  the angle of misorientation. In agreement with experimental results, see fig.4.  Similar results have been published by Kendall.  However, the situation close to the <l00> directions is  unclear. In the <l00> - direction there is also a minimum if one etches silicon in KOH and NaOH. In  situations where the minimum is steep enough it is  possible to micromachine vertical <l00> walls in <001>  oriented wafers. Mirror like flat {l00)-faces have  been reported  at particular etching conditions (35  wt% KOH, 80 "C). Possibly the (100) are flat under  these conditions in which case eq. (1) would apply.

Fk. 4. A screw dislocation gives rise to a step on the crystal  surface (a). The step moves when the crystalgrows (b) and if  it is etched (c)

IV. DISCUSSION  

The minimum of the etch rate at the <l00> direction  implies in our view that the {l00} faces are flat when  they are in contact with KOH solutions investigated in  our experiments. This is only possible if the surfaces are  either reconstructed or if there is an adsorption layer on  the {l00} faces that stabilise in some way the surface . To our best knowledge, this is the first time that  some evidence of surface reconstruction of silicon  surfaces in contact with an etching solution is given.  Certainly, the step free energy on {l00} is considerably  smaller than on the I1111 faces, as evidenced by the  large etch rate of the {l00}. This is consistent with the  absence of high steps on slightly disoriented {l00} faces.  These high steps are created by "collisions" of steps, a  process that is strongly enhanced by adsorption of  impurities at the surface .