马兰戈尼干燥模型

Marangoni drying is a new ultra-clean drying process, which relies on surface-tension gradient forces, so-called Marangoni stresses. This method is of particular use in the semiconductor industry wherein obtaining ultra-clean surfaces is of paramount importance. The present work provides a mathematical description of this novel process involving four coupled partial differential equations, derived in the thin-layer approximation, for the film thickness, the concentration of chemicals in the air, at the air–liquid interface and in the bulk of the liquid film. Numerical solution of these equations yields prediction of typical profiles that accompany the spreading and drying processes. Particular attention is aimed at the prediction of the minimum film thickness as a function of system parameters with a view to optimizing the drying process.

I. INTRODUCTION 

Marangoni drying is a relatively novel technique employed in obtaining ultra-clean surfaces in the semiconductor industry. Recently developed at the Philips Research Laboratories,this technique is based on the so-called Marangoni effect in the following way: if the vertical withdrawal of a semiconductor wafer from a pool of liquid is carried out in the presence of an organic vapor, and if this vapor, upon adsorption at the air–liquid interface, can in turn induce a local reduction in the surface tension, i.e., act as a surfactant thereby giving rise to gradients in surface tension, then Marangoni flow will result. Flow due to the Marangoni effect proceeds from regions of lower surface tension high concentration of the organic chemical! to those of higher surface tension low concentration of chemical . If the vapor source is held near the liquid film in the vicinity of the three phase line away from the liquid pool, then Marangoni forces will drive flow away from the three-point line towards the liquid pool. This flow will reinforce that due to gravitational drainage giving rise to enhanced drying, leaving behind a thin liquid film with thickness of order 0.01–0.1 m m.3,6 The advantages that Marangoni drying enjoys over conventional processes such as, for instance, spin drying are those of efficiency and cleanliness. This method avoids contamination of the wafer surface that can occur either due to the action of the centrifuge or from the passage of contaminants from the liquid to the substrate following evaporation of the liquid at the final stages of the drying process.

Incidentally, Marangoni drying drives fluid off the substrate, back into the bath of fluid, and has the opposite effect to the classic “tears of wine” effect, originally described by Thomson, whereby alcohol evaporation from wine in the meniscus region also leads to surface tension gradients, this time drawing fluid from the bath up the edge of the glass. In both cases it is testament to the sensitive behavior of surface tension upon surfactant either absorbed onto, or evaporated from, the interface that these surface tension gradient effects are so pronounced.

II. THE MODEL 

We consider the withdrawal of a flat infinitely long plate from an unbounded reservoir of Newtonian liquid, with constant velocity, U0 , as shown in Fig. 1. Distance along the plate is denoted by x ~ x increases from the origin, located at the meniscus, in a direction up the plate! while distances perpendicular to the plate are denoted by z. Note that we shall use a different vertical coordinate, y, above the liquid film, as shown in Fig. 1.

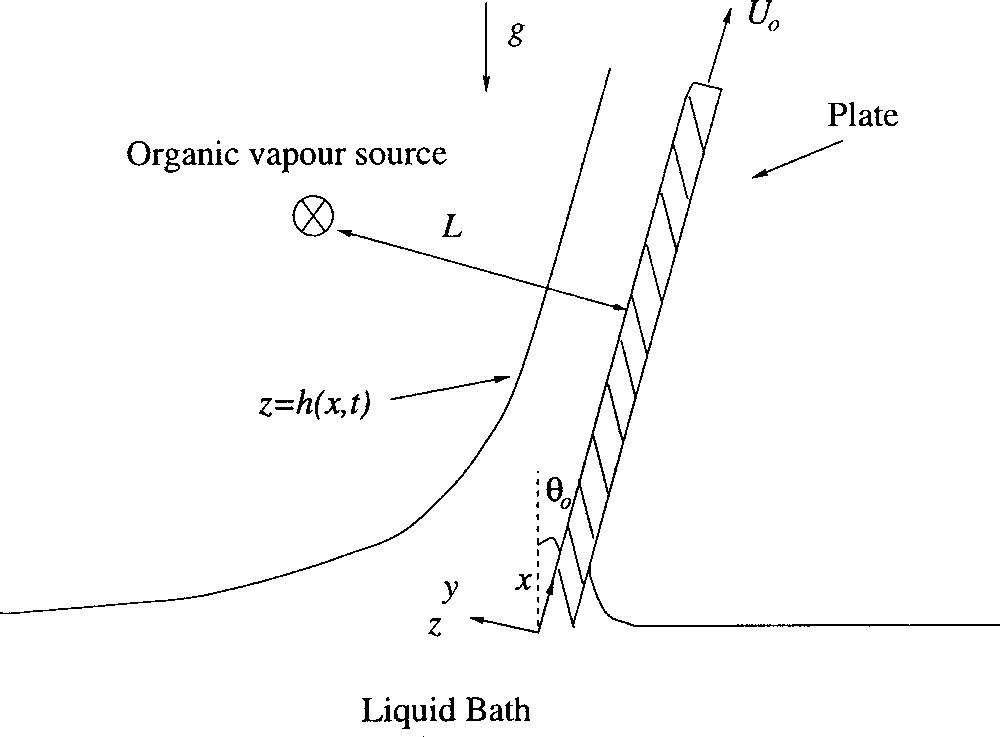
A thin film of liquid of characteristic thickness H, density r , and viscosity m is entrained by the motion of the plate, which is inclined at an angle u 0 to the vertical, being thinnest in the region furthest from the reservoir. Only cases corresponding θ₀=0, however, will be considered in the subsequent analysis. A line source is placed a perpendicular distance, L, from the plate and supplies organic vapor. The strength of this source, λ, is prescribed, for instance, if the source is switched on at time zero and maintained at a constant value in time thereafter, then the surfactant is added to the system at a rate l per unit time. The source position, x0 , y 0 , is prescribed; we choose y 05 from the fluid bath, x0 , to vary.

Ⅲ.Discussion of reduced model predictions

In Figs. 3 and 4 we show results of numerical simulations investigating the variation of St1 , that is, the rate at which chemical is adsorbed relative to the characteristic Marangoni velocity. These figures also contain a comparison between results obtained using the "decoupled" and‘’passive liquid film' models. Figures 3 and 4 show that the severe peaks of the decoupled model are modified by the presence of surfactant transport. This is more pronounced in Fig. 3, which is for the lower adsorption ratio of chemical to velocity. The fully decoupled model can be recovered by uncoupling the surfactant equation with St15 k1 /V@ 1 while the ratio b 35 k3 /k1 remains a constant partition coefficient. Indeed in Fig. 4 one can see this limiting process, with the severe peaks in the passive liquid film model.

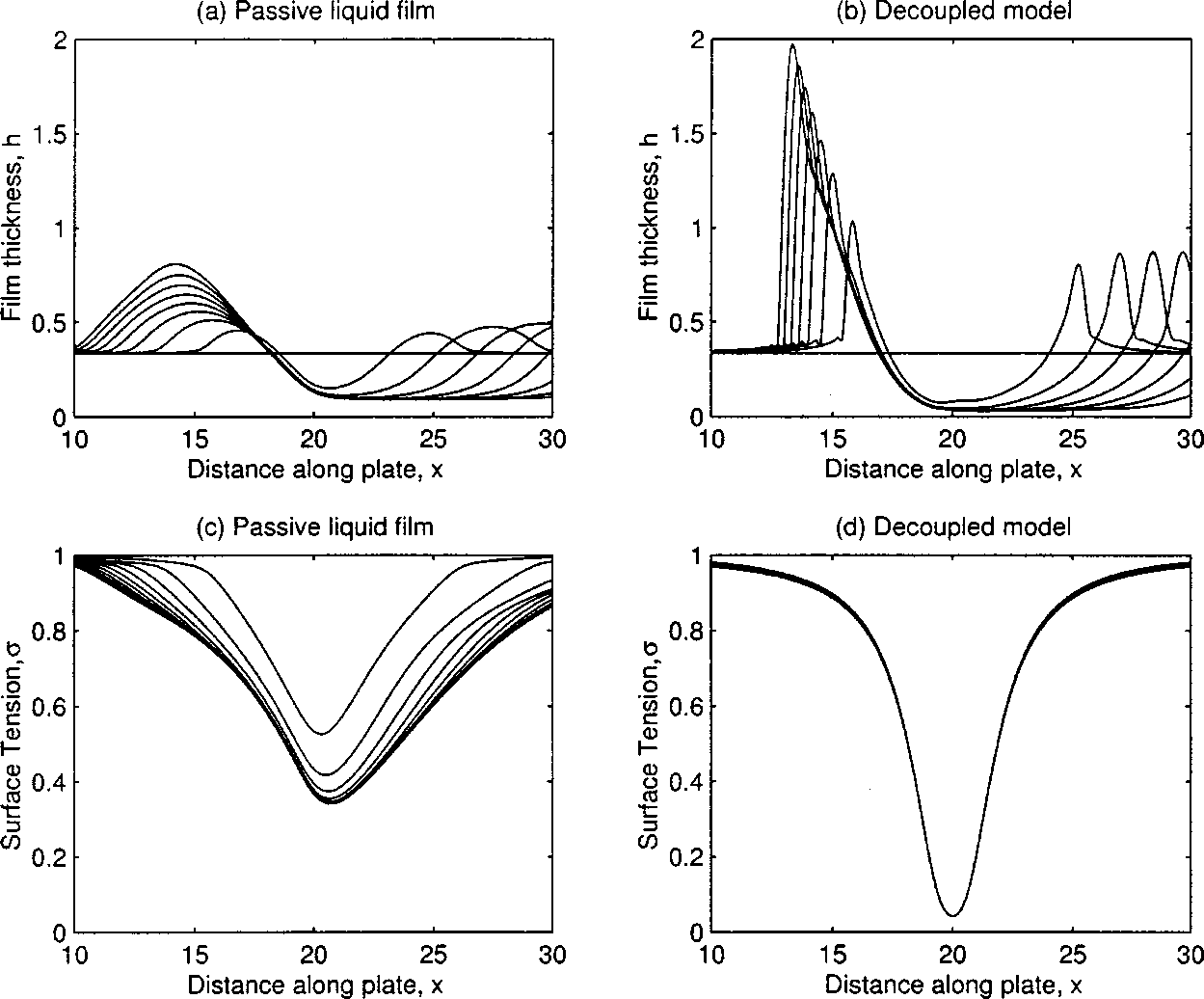
FIG. 3. 

Ⅳ. CONCLUSIONS 

We have developed a mathematical model for Marangoni drying in the lubrication approximation that takes full account of chemical transport from the gas phase to the interface, along the interface and from the interface to the bulk, and accompanying interfacial deformation. The model comprises three coupled nonlinear partial differential equations for the liquid film thickness and the chemical concentration at the interface and in bulk, driven by a linear transport equation for the chemical in the gas phase; the chemical is delivered to the film surface from a line source in a quiescent environment. In this model, the surface tension is coupled to the interfacial concentration by a nonlinear equation of state,8 in which different chemicals are parametrized by the nonlinearity in this relation. The initial condition for the film thickness is taken to be the steady solution of the plate withdrawal problem in which the solution of the stationary plate16 is dynamically adjusted to the asymptotic result of Landau and Levich9 for a finite velocity of withdrawal. Several limits of the model have been explored, but we have focused on the main limit of interest for this application: rapid chemical adsorption, characterized by a large Stanton number, St15 k1 /V@ 1, and slow desorption from the interface back to the gas, b 25 k2 /k1 1. In this limit, the process is primarily characterized by St1 and St35 k3 /V, which measures the relative significance of chemical desorption from the interface to the bulk relative to the characteristic Marangoni velocity.

The primary interest is in the thinning of the liquid, and its parametric dependence on the nonlinearity in the equation of state, the mass transfer coefficients in all phases, and velocity of plate withdrawal, among other parameters; we have investigated these effects on the minimum film thickness. Our primary conclusion is that maximal efficiency would appear to require large values of the nonlinearity although it is possible that such values may lead to uneven drying! and low values of b 35 St3 /St1 and of the plate velocity. We have also found that, in the limit of rapid adsorption, the minimum thickness is weakly dependent on the parameter St1 . Subsequent details, such as the rate at which chemical is desorbed into the bulk, are less important, especially in cases wherein the chemical is easily readsorbed by the interface.