高通量在线硅晶圆检测中的定量剪切应力成像

ABSTRACT  

Defect inspection methods are basic steps in electronic chip manufacturing and power device production processes in the semiconductor industry. Based on stress induced photoelastic anisotropy, in-line polarized stress  imaging (PSI) and quantitative determination of the local shear stress component are possible in single crystalline  silicon wafers. Hereafter, such polarization stress images are compared and validated quantitatively with results  of finite element simulations based on different 3D elastic models. Uniquely, high resolution at high throughputs  is achieved for 300 mm wafer size in the present quantitative stress imaging study.

1. Introduction  

Defect inspection methods are basic steps in electronic chip  manufacturing and power device production processes of the semiconductor industry. Based on these methods, practically dislocation free  Si wafers and epitaxial layers can be produced in various applications by  sorting out defected areas or wafers and optimizing ion implantation  and thermal treatment steps. Polarization imaging is widely accepted  among such defect inspection methods because of its nondestructive  nature based on the phenomenon of stress induced birefringence. Polarization imaging methods were used successfully to identify small  defects, even single dislocations, in wide band gap semiconductor materials such as GaN , SiC , Ba(NO3)2  and diamond.

If section of the indicatrix with the plane normal to the light propagation is an ellipsis (indicated by yellow color in Fig. 1), birefringence  produces phase delay (δ) between the polarization components of the  light wave. Parameters of this ellipsis can be readily obtained as B* ijrirj = 1 by a projection of Bij into B* ij, if the light wave propagates along one  axis of the coordinate system (e.g. along z axis as shown in Fig. 1).

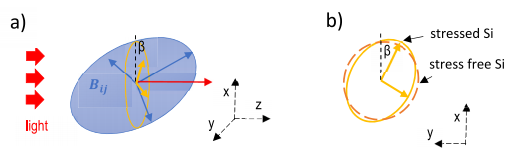
Fig. 1. (a) Schematic image explaining light birefringence in Si. The blue ellipsoid is the indicatrix, with the principal axes of Bij (blue vectors). Intersection of the  indicatrix with the normal plane of light wave is indicated by a yellow ellipsis. (b) Major and minor axes of the ellipsis and angle of the major axis (β) are also  indicated in the x-y plane section for isotropic stress free Si (dashed line) and for stressed Si (solid line).

Polarization imaging can be carried out by a polariscope. Such a  polariscope consists of mostly a polarizer, the sample and an analyzer  plate. Additionally, quarter wave plates (QWP) are also placed between  the sample and the different polarizer plates (named as general or circular polariscope) as shown in Fig. 2. If absorption of the sample and the  different optical elements is neglected, the orientation of these optical  elements together with the δ (phase difference) and the β (angle of the  main axis of birefringence) determine the intensity ratio of the detector  and the incident light (I/I0). 

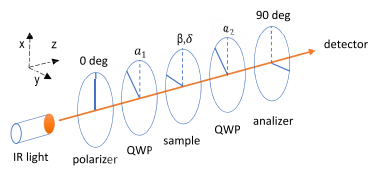
Fig. 2. Optical model of a general dark field polariscope with polarizer, two  quarter wave plates (QWP), analyzer and the sample. Parameters of the optical  elements are also indicated.

For the present polarization stress imaging, a 300 mm size 100 Si  wafer, which was free from large defects, was used. The wafer was held  by three grips, which were aligned approximately equal distances along  the circumference of the wafer. One grip applied radial force (F) to the  wafer in perpendicular direction to the [110] wafer notch, while the two  other grips fixed the position of the wafer (see Fig. 3a). This geometry, in  principle, is similar to the so called Brazilian test, which is used for photo-elastic calibration in the literature.

Polarization stress imaging was carried out using the PSI-3100  equipment with different F forces in the 0–0.7 N range. A couple of  PSI images acquired by F––F0 (initial grip force) and F––F0+0.4 N  (enhanced grip force) are shown in Fig. 3b and c, respectively. As seen,  the radial forces along the perimeter produce strong patterns, which  account for the stress induced birefringence in the Si wafer. Additionally, smaller stress lobes (right from the upper left and also right from  the lower left grips), which account for internal defects along the wafer  edge, are also visible in Fig. 3b and c. To tests the reproducibility of the  imaging method the measurements were repeated several times (see  Supplementary S1).

Fig. 3. a) Schematic of the edge gripped 300 mm diameter wafer with two fixed grips and one grip applying constant F force. Notch indicates the [110] direction for  a (001) wafer plane (100 wafer). PSI images of a 100 wafer with grip force of b) F––F0 and c) F––F0+0.4 N.

In the present work, results of an isotropic (Young modulus of E = 170 GPa and Poisson’s ratio of ν = 0.28) FE model and a cubic or  anisotropic (C11 = 165.7 GPa, C12 = 63.9 GPa and C44 = 79.6 GPa)  elastic FE model are presented. Further details on the FE modelling can  be found in the Supplementary S2. To be conform with the PSI geometry  and Equation (10), the z averaged in-plane stress components (σ11, σ22  and σ12) are shown in Fig. 4 for both models. Integration and part of the  postprocessing was performed in python.

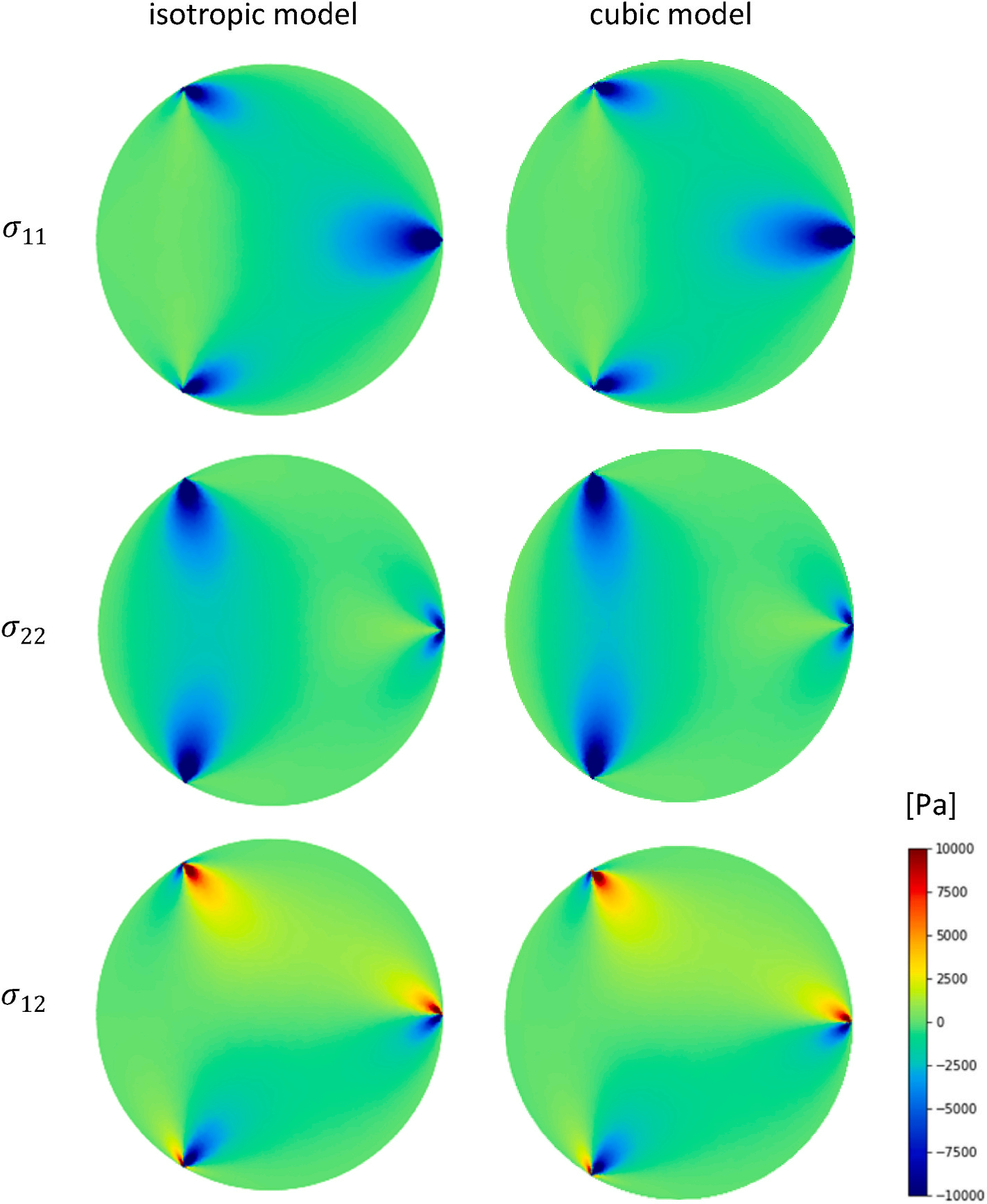
Fig. 4. In-plane σ11(x, y), σ22(x, y) and σ12(x, y) stress components obtained from FE simulations with isotropic and cubic models. Each stress components were  averaged over the wafer thickness and were obtained from the same FE simulation with F = 0.4 N grip force.

To validate the FE results and reveal the symmetric/asymmetric effect of the three grips in the isotropic/anisotropic cases, the von Mises  stress component is also plotted for the two models in Fig. 5. The von  Mises stress shows threefold symmetry and circular stress levels as it is  anticipated from the theory of Hertzian contact for isotropic solids ,  while this symmetry is broken slightly in the cubic (anisotropic) Si  wafer.

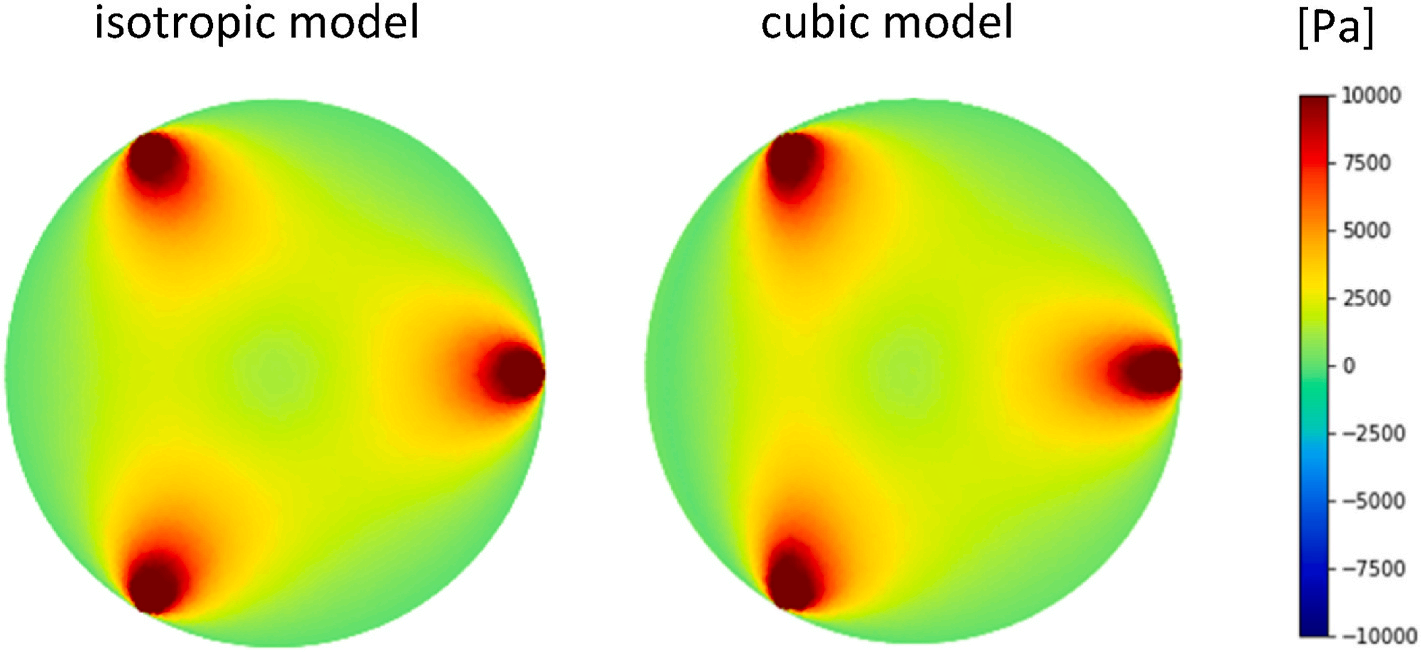
Fig. 5. The von Mises stress averaged over the wafer thickness as determined from the FE simulations for isotropic and cubic models with F = 0.4 N.

Conclusion 

 Common high throughput and high resolution stress imaging was  performed in the present work using a special in-line polariscope. For  comparison with similar stress imaging equipments, a quantitative  measure for the information production was proposed. Stress patterns of  an edge gripped 300 mm wafer was measured experimentally for  different edge loads and compared to the results of Comsol finite  element simulations. Quantitative comparison was made between the  experimental and the simulation results and, accordingly, whole wafer  polarized stress images with fine details on the shear stress distribution  of individual defects were presented. For 100 Si wafers, analytical  connection was proved between the stress field of the defects and their  observed intensity distribution.