Abstract: Microfabrication technology with quartz crystals is gaining importance as the miniaturization of quartz MEMS devices is essential to ensure the development of portable and wearable electronics. However, until now, there have been no reports of dimension compensation for quartz device fabrication. Therefore, this paper studied the wet etching process of Z-cut quartz crystal substrates for making deep trench patterns using Au/Cr metal hard masks and proposed the first quartz fabrication dimension compensation strategy. The size effect of various sizes of hard mask patterns on the undercut developed in wet etching was experimentally investigated. Quartz wafers masked with initial vias ranging from 3 µm to 80 µm in width were etched in a buffered oxide etch solution (BOE, HF:NH4F = 3:2) at 80 ℃ for prolonged etching (>95 min). It was found that a larger hard mask width resulted in a smaller undercut, and a 30 µm difference in hard mask width would result in a 17.2% increase in undercut. In particular, the undercuts were mainly formed in the first 5 min of etching with a relatively high etching rate of 0.7 µm/min (max). Then, the etching rate decreased rapidly to 27%. Furthermore, based on the etching width compensation and etching position compensation, new solutions were proposed for quartz crystal device fabrication. And these two kinds of compensation solutions were used in the fabrication of an ultra-small quartz crystal tuning fork with a resonant frequency of 32.768 kHz. With these approaches, the actual etched size of critical parts of the device only deviated from the designed size by 0.7%. And the pattern position symmetry of the secondary lithography etching process was improved by 96.3% compared to the uncompensated one. It demonstrated significant potential for improving the fabrication accuracy of quartz crystal devices.
1. Introduction
Quartz crystal has become the most widely used piezoelectric material distinguished by its excellent physical and chemical properties. Since Statek applied MicroElectro-Mechanical system (MEMS) process technology to the fabrication of quartz crystal devices for the first time in 1973, quartz MEMSs (QMEMSs) provided a good starting point for all kinds of sensors and actuators, such as gyroscopes, accelerometers and oscillators. Since then, wet etching in fluoride-based solutions has been one of the most fundamental QMEMS techniques used in the process of fabricating quartz devices.
Wet etching is advantageous when compared to dry etching due to its low cost. However, undercuts between the quartz substrate and metal hard mask (Au/Cr films are the most commonly used) caused by etchants during the fabrication of the quartz microstructures became an unavoidable but undesired phenomenon. As shown in Figure 1a, the undercut in the X direction reached 12.3 µm and 6.7 µm, respectively, for a trench with a hard mask width of 70 um etched in 100 min. And the actual trench widthreached 83.4 um with an increase of 19.14% compared to the designed size, which changedthe actual size of the device and had a serious impact on the precision of the fabricationThese variations in dimensions could even affect the functionality of the microstructure.

Fig1
Figure lb shows the ultra-small quartz MEMS tuning fork oscillator in our studies.The device was fabricated on a Z-cut quartz wafer. As shown in Formula (1), the frequency ofthe tuning fork was significantly determined by the form size.
As shown in Figure 1e, the resonant impedance of the tuning fork showed a clear quadratic relationship with Doffset. And even small position offsets could influence the resonant impedance markedly. An offset of 5 µm resulted in a frequency deviation of nearly 21,300 ppm (700 Hz), which was much worse than the market demand for that of less than 8 ppm (2.6 Hz). Thus, position fabrication errors caused by anisotropic undercuts had an extremely noticeable effect on the functionalities of devices. Therefore, it was particularly important and necessary to consider the undercut and dimensional compensation in process design.
2. Materials and Methods
If the device size is large enough, the initial hard mask width can be changed enough to match the device size. And the difference in hard mask width is meaningless for etching ultra-small quartz devices. Therefore, this work focused on fourteen ultra-small hard mask widths (<100 µm), which are more valuable for improving the etching precision of ultra-small resonant devices. The initial long-strip pattern widths ranged from 3 µm to 80 µm and were divided into 3 groups, A (3 µm, 5 µm), B (from 10 µm to 45 µm in intervals of 5 µm), and C (from 50 µm to 80 µm in intervals of 10 µm) (Figure 2a). All the long strips were 1 mm in length and 50 µm apart, pointing to the Y direction. And the samples were etched with different etching times.
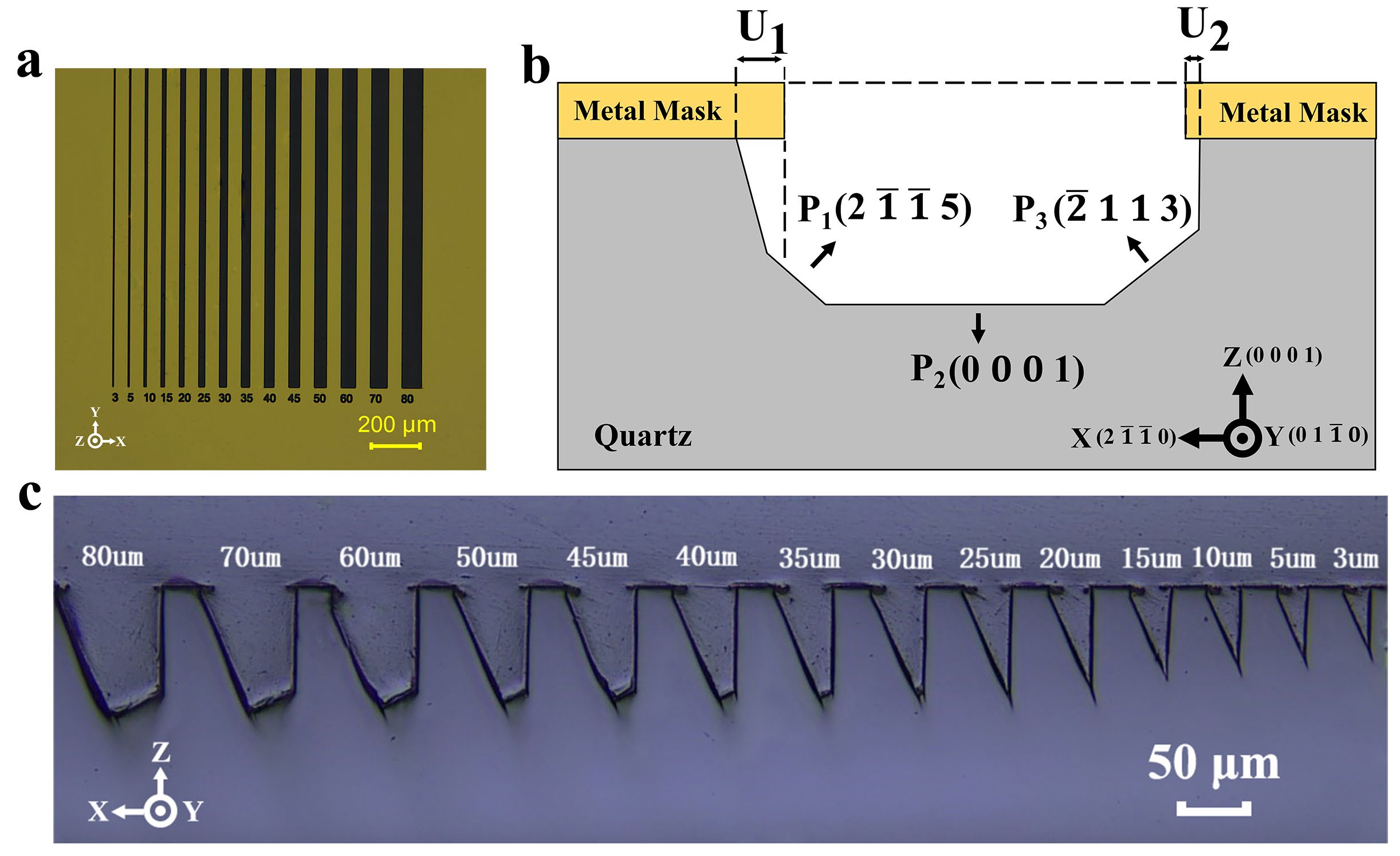
Fig2
Although Hedlund and Liang have already reported the definition of a Z-cut quartz plane etched profile morphology, this definition was only suitable for macroscopic descriptions of etching results with large hard mask widths. For the purpose of this work, a novel and concise definition was proposed to satisfy the characterization of small-hardmask-width etching profiles. As shown in Figure 2b, a complete bilateral etched groove is demonstrated in this work, which is different from previous work where only half of the etched profile was defined. And angles were not imported into the definition, which would greatly simplify the characterization of the etching profile. Instead, three planes were defined (P1(2115), P2(0001), P3(2113)), which made it easier to present the evolution of the etching profiles. In particular, this work made full use of undercuts to design a new fabrication compensation process; therefore, the depths of the undercuts were exclusively represented by U1 and U2, respectively. This definition of the profile focused the variables on characterizing the complete evolution of the etching groove itself, rather than the individual etching rate, which would facilitate the hard mask width to enable the design of a number of novel processes in practical engineering applications.
Finally, Figure 17a shows the ultra-small tuning fork device fabricated in this workFor size illustration, the device was placed next to a rice grain. The tuning fork was testedby an impedance analyzer at normal atmospheric pressure, and Figure 17b illustrates thetesting results. It is worth noting that with these meticulous compensation strategies, itwas even possible to use the metal deposition and laser frequency tuning processes, whichgreatly enhanced production efficiency. Furthermore, a tuning fork manufactured by acertain company was used for comparison. The impedance of this working tuning forkwas 8.7% lower and the quality factor Q was 54.6% higher than that ofthe comparison one.
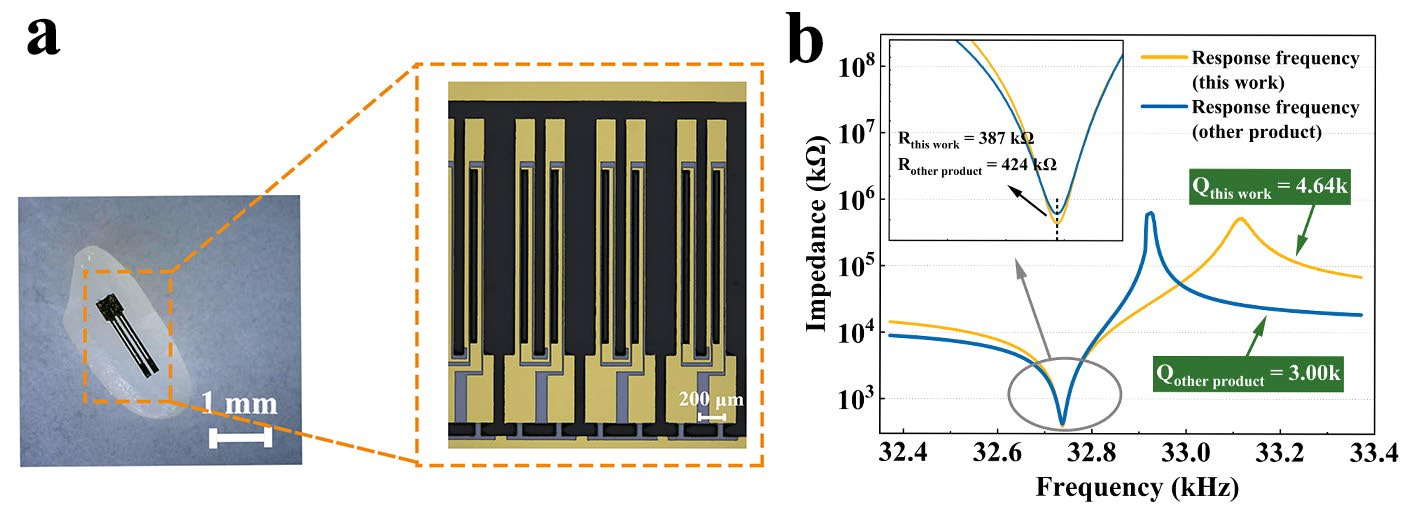
Fig17
3.Conclusions
In this work, we focused on the size effect of the undercut on the Z-cut quartz crystalin wet etching, experimentally summarized the etching patterns, and came up with twokinds of dimensional compensation strategies to fabricate a kind of ultra-small quartzcrystal tuning fork resonator. In this process, the complete bilateral etching morphologywas defined, and the etching depth and rate of undercut were used to characterize thesize effect on the etching results. lt was found that the undercut U, in the +X direction fordifferent initial widths grew almost linearly with etching time. The initial width beganto have a significant effect on the etching results after 95 min of etching. The larger theinitial width, the smaller the U,. The undercut U, in the -Xdirection showed differentlaws. During the first 80 min, U2 increased approximately linearly with etching time, butafter 80 min, the increase rate became slower. A larger initial line width also resulted ina smaller U2 after 100 min. Interestingly, by calculating the etching rate of the undercutwe found that the undercut was formed almost in the first 5 min with a relatively highetching rate. After that, the etching rate began to increase rapidly from 15% to 27%. Andthe average etching rate of the undercut in the +X direction was almost twice as high as thatin the -X direction. Afterwards, these etching laws were employed to develop two typesofdimensional compensation solutions, etching width compensation and etching positioncompensation. And an ultra-compact quartz resonator with a frequency of32.768 kHz wassuccessfully fabricated by using
上一篇: 硅片上集成微电子和光子电路