硅各向异性湿法刻蚀剖面演化的三维模拟

1. Introduction

Refifined control of etched profifiles is one of the most important tasks of MEMS manufacturing process. In spite of its wide use, the simulation of etching for MEMS applications has been so far a partial success only, although a great number of commercial and academic research tools dedicated to this problem are developed. Level set method, introduced by Osher and Sethian [1], is a powerful technique for analyzing and computing moving fronts in a variety of different settings. The level sets are used in image processing, computer vision, computational flfluid dynamics, material science, and many other fifields. Detailed exposition of the theoretical and numerical aspects of the method, and applications to different areas can be found in books [1] and [2]. Some of our previous results describing the implementation of this methodology to the dry etching process can be found in [3]. The level set methods for evolving interfaces are specially designed for profifiles which can develop sharp corners, change of topology and undergo orders of magnitude changes in speed. In this paper we describe shortly the level set method as well as sparse fifield method for solving the level set equations. The sparse-fifield method itself, developed by Whitaker [4], and broadly used in image processing community, is an alternative to the usual combination of narrow band and fast marching procedures for the computationally effective solving of the level set equations. After that we analyze the case of non-convex Hamiltonians and its application in the simulations of the etching profifile evolution during anisotropic wet etching of silicon with KOH etchant in more details.

2. Sparse fifield level set method The basic idea behind the level set method is to represent the surface in question at a certain time t as the zero level set (with respect to the space variables) of a certain function φ (t, x), the so called level set function. The initial surface is given by {x|φ (0, x)= 0}. The evolution of the surface in time is caused by “forces” or flfluxes of particles reaching the surface in the case of the etching process. The velocity of the point on the surface normal to the surface will be denoted by R(t, x), and is called velocity function. For the points on the surface this function is determined by physical models of the ongoing processes. The velocity function generally depends on the time and space variables and we assume that it is defifined on the whole simulation domain. At a later time tN0, the surface is as well the zero level set of the function φ (t, x), namely it can be defifined as a set of points xaRnju t;x ð Þ = 0 f g. This leads to the level set equation Au At + R t; x ð Þjjuj = 0 ð1Þin the unknown function φ (t, x). Having solved this equation the zero level set of the solution is the sought surface at all later times. The sparse-fifield method use an approximation to the level set function that makes it feasible to recompute the neighborhood of the zero level set at each time step. In that way, it takes the narrow band strategy to the extreme. It computes updates on a band of grid points that is only one point wide. This approach has several advantages. The algorithm does precisely the number of calculation needed to compute the next position of the zero level set surface. The number of points being computed is so small that it is feasible to use a linked-list to keep a track of them, so at each iteration only those points are visited whose values control the position of the zero level set surface. As a result, the number ofcomputations increases with the size of the surface, rather than with the resolution of the grid. The Eq. (1) can be rewritten in Hamilton–Jacobi form Au At + H ju t; x ð Þ ð Þ = 0; ð2Þ where Hamiltonian is given by H = V t; x ð Þjju t; x ð Þj (in this context the term “Hamiltonian” denotes a Hamiltonian function, not an operator). We say that such a Hamiltonian is convex (in Rn ) if the following condition is fulfifilledwhere φxi is a partial derivative of φ(t,x) with respect of xi. If the surface velocity R (t,x) does not depend on the level set function φ(t, x) itself, this condition is usually satisfified. In that case the spatial derivatives of φ can be approximated using the Engquist–Osher upwind fifinite difference scheme, or by ENO (higher-order essentially non-oscillatory) and WENO (weighted essentially nonoscillatory) discretization schemes, that requires the values of this function at the all grid points considered. The resulting semidiscrete equations can be solved using explicit Euler method, or more precisely by TVD (total-variation diminishing) Runge–Kutta time integration procedure (see Refs. [1] and [2] for the details). The non-convex Hamiltonians are characteristic for anisotropic wet etching, plasma etching and deposition simulations. The upwind fifinite difference schemes cannot be used in the case of non-convex Hamiltonians, since they are derived under the assumption of convexity (see paragraph 5.2.2.3 of Ref.[1]). The simplest scheme that can be applied in these cases is the Lax–Friedrichs, one which relies on the central difference approximation to the numerical flflux function, and preserves monotonicity through a second-order linear smoothing term:

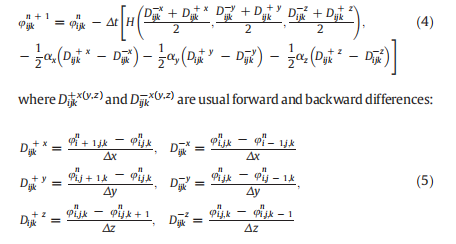
and αx(αy, αz) is a bound on the partial derivative of the Hamiltonian with respect to the fifirst (second, third) argument:

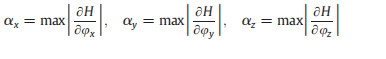
The terms on the second row of the above equation are the smoothing terms. They are similar to the second derivatives in each variable. In general, these terms need not be calculated exactly. Overestimated values will produce non-realistic smoothing of the sharp corners in the implicit surfaces. Too little smoothing usually leads to numerical instabilities in calculations. In Ref. [5] it is shown that it is possible to use the Lax–Friedrichs scheme in conjunction