化合物半导体纳米粒子的表面键合效应

This is a preprint of a paper intended for publication in a journal or  proceedings. Since changes may be made before publication, this  preprint should not be cited or reproduced without permission of the  author. This document was prepared as an account of work  sponsored by an agency of the United States Government. Neither  the United States Government nor any agency thereof, or any of  their employees, makes any warranty, expressed or implied, or  assumes any legal liability or responsibility for any third party’s use,  or the results of such use, of any information, apparatus, product or  process disclosed in this report, or represents that its use by such  third party would not infringe privately owned rights. The views  expressed in this paper are not necessarily those of the United  States Government or the sponsoring agency.

Small nanoparticles have a large proportion of their atoms either at or near the surface,  and those in clusters are essentially all on the surface. As a consequence, the details of  the surface structure are of paramount importance in governing the overall stability of the  particle. Just as with bulk materials, factors that determine this stability include “bulk”  structure, surface reconstruction, charge balance and hybridization, ionicity, strain,  stoichiometry, and the presence of adsorbates. Needless to say, many of these factors,  such as charge balance, hybridization and strain, are interdependent. These factors all  contribute to the overall binding energy of clusters and small nanoparticles and play a  role in determining the deviations from an inverse size dependence that we have  previously reported for compound semiconductor materials. Using first-principles  density functional theory calculations, we have explored how these factors influence  particle stability under a variety of conditions.

The binding or cohesive energy of nanoparticles is of importance because it determines a  wide range of physical properties including melting point, congruent vapor pressure,  sintering rate and solubility. This is especially true in the case of smaller particles where  these properties are often difficult to determine experimentally. Fortunately, first  principles theoretical calculations using, for example, density-functional theory can be  used to obtain nanoparticle energies with a reasonable degree of accuracy. From these  theoretically obtained energies, many relevant physical properties can be estimated to  supplement the experimental situation. Furthermore, such calculations can now be  performed relatively easily, particularly in the small size range where experimental  determinations are most difficult.

Previously, we have shown that, unlike most metals, the per-atom-pair binding energy of  compound semiconductor clusters and small nanoparticles is not a linear function of the  inverse of the particle diameter or radius . It is, rather, closer to a quadratic  dependence, and the per atom-pair binding energy approaches that of the bulk material  more rapidly with increasing size than for most metals. This behavior is similar to  that of the elemental semiconductors, C, Si and Ge, and of the Group IV metals, Sn and  Pb. Interestingly enough, it also resembles the non-linear inverse size dependence  seen for metal oxides.

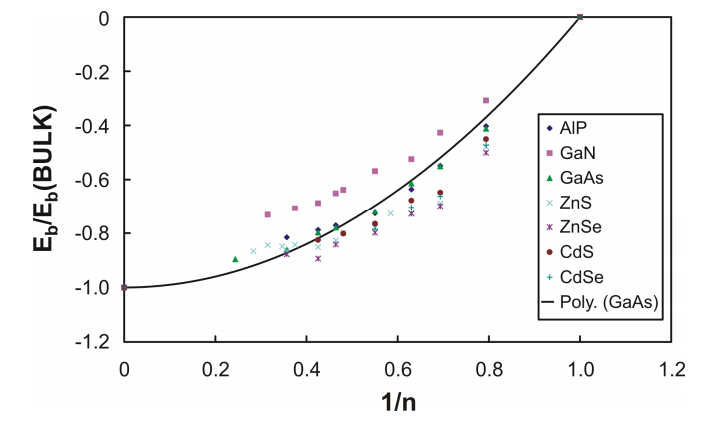
Fig1

To summarize our earlier results, in Figure 1 are shown the normalized, per atom-pair  (M-X) binding energies as a function of 1/n for AlP, CdS, CdSe, GaN, GaAs, ZaS, and  ZnSe. In order to show all of the data on the same graph, they are plotted as a function of  both reduced energy and reduced reciprocal radius. Normalization of the energy along  the y-axis was achieved by dividing the particle per atom-pair binding energies by that  for the bulk, and referencing that to the energy for a single pair of M-X atoms. In  addition, we have, in essence, normalized the reciprocal size along the x-axis as well by  using 1/n, where n is the cube root of the number of atom-pairs in the cluster or  nanoparticle, as our variable. Here, n = r/r₀ where r is the effective radius of the particle  and r₀ is the average radius of a single pair of M-X atoms. Noting that, at least for low  aspect-ratio particles, n scales with r, the radius of the particle, this graphic representation is equivalent to plotting the per-atom binding energies as a function of the reduced  inverse size of the particles. In Figure 1, the point on the far right of the diagram refers to  a single atom-pair (n = 1) while the point on the far left refers to the bulk material (n =  ∞ ).